x2-11x+28=0, algebraic mathematical expression is a quadratic equation. Quadratic equations are those mathematical equations which have the highest exponential power of 2. In this article, we will understand more about quadratic equations, their structure and how to solve them.
x2-11x+28=0: Introduction
x2-11x+28=0 is a second degree algebraic expression. It is also called the quadratic equation. Word quadratic is derive from a word of Latin language, quadratus . It means the square. It indicates the power 2 in the equation. Quadratic equations are of very much use in different fields of physics, astronomy, engineering etc. When we solve any quadratic equation, we can find two possible solutions for a quadratic equation. These two solutions are places as the value of ‘x‘ in the equation. The first solution is denotes as ‘alpha’ and the other solution is denotes as ‘beta’.
Quadratic Equation And Its Structure
The quadratic equations are those which can be written in the standard form of a quadratic equation. You can find them written in another form also, but these could be solve to write in the standard form. An algebraic equation of second degree in x is termed as a quadratic equation. The structural formula for a quadratic equation is ax²+bx+c=0. Here, x is the variable. A and B are coefficients and C is the constant in the equation. In a quadratic equation, the coefficient of x² cannot be zero.
Roots Of Quadratic Equation
- Roots of quadratic equations are substituted as values of x in the quadratic equations for satisfaction. These two values can be determine using different methods which we will explain below. The two values of x are denoted as alpha and beta roots. The quadratic formula:
- X=(-b+√(b²) – 4ac)÷ 2a
- X=(-b-√(b²) – 4ac) ÷ 2a
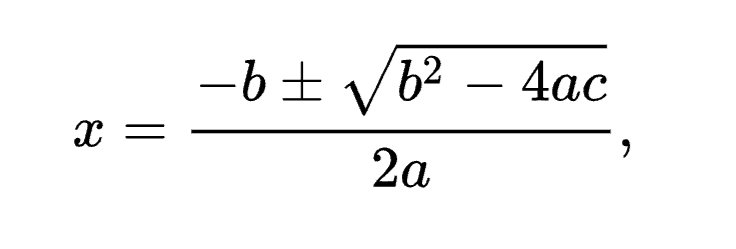
- The quadratic formula is the simplest method of determining the roots of a quadratic equation. All you need to do is find out the values of a, b and c from the quadratic equation and put it into the quadratic formula. This quadratic formula is singly able to be use to find both the zeros of the quadratic equation with just changing the positive – negative signs in the formula.
Finding Up The Roots
Finding roots of the x2-11x+28=0 can be done by using the four different methods. One of them we are familiar with in the above part i.e using the quadratic formula. The all four methods which can be use to find out the roots of a quadratic equation are as given below:
- Using quadratic formula
- Using factorization method
- Using method of completing the square
- Using graphical method to find the roots
- Using quadratic method: We studied this method in the above part. We need to place the values of a, b and c in the quadratic formula and we will get the values of x by using + and – sign in two times.
- Using factorization method: Factorization involves a few steps to find out the roots of the quadratic equations. It involves breaking the middle term into two parts so that the sum of the two parts is equal to the constant term and then we can solve the equation further using the step method as illustrated below:
- X²+(a+b)X +ab=0
- X²+aX+bX+ab=0
- X(X+a) +b(X+a)=0
- (X+a)(X+b)=0
- Using method of completing the square: It is a long method and generally not preferred over the factorization method and formula method. In this method, you have to isolate that term which has the squared variable. After that you have to take the square root of both sides to solve and find out the roots.
- Using graphical method to find the roots: In the graphical methods, the roots of the equation are recognized as the values of the x- coordinates where the function crosses the x-axis. These points are termed as x intercepts. In order to solve a quadratic equation using the graphical method.
- Firstly you have made zero on one side of not already given.
- Then draw the graph for the quadratic function.
- Read the x coordinates and get the values of the roots of the equation.
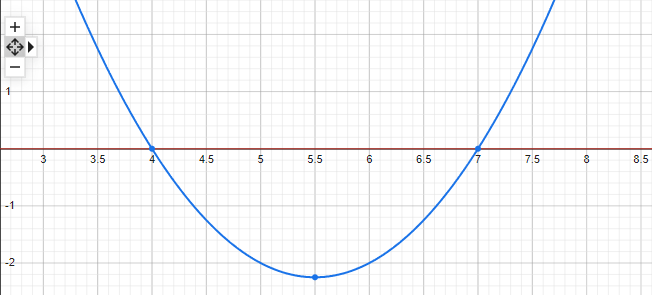
Solution Of x2-11x+28=0
We have x2-11x+28=0,
Now apply quadratic formula to get the solution
we get a=1, b= -11, c=28; put these value into below formula.
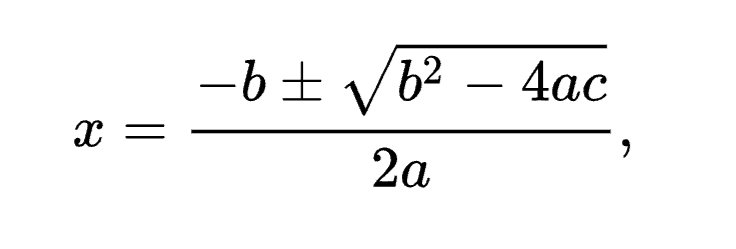
- x={(-11)2 ± √(-11)2 -4*1*28}÷ 2*1
- x= (11 ± 3)/2
- x= (11 + 3)/2 or x= (11 – 3)/2
- x= 7 or x = 4
Graph:
Discriminant And Nature Of The Roots In A Quadratic Equation
The nature of the roots of a quadratic equation are determine using the discriminant value of the equation. The discriminant value is denote by ‘D’. It is determine using the given formula.
- D=b²-4ac
The value of D resembles the nature of the roots in following way:
- If the value of D is more than 0, the roots are real and distinct.
- If the value of D is equal to 0 then the roots are real and equal.
- If the value of D is less than 0, the roots are imaginary or they do not exist.




